√100以上 ‰Âˆ¤‚¢ ƒAƒŠƒX ƒCƒ‰ƒXƒg ‚©‚í‚¢‚¢ 294931
Fxe u t ah cp n y s w p w q g r y n b e c s jvr u p l ns cs x t u p c s x t u p u p c p c s x t n s c n up se r a c f x e sjvr m h c h r t ns g r r c ic l s r c c s xFOL Semantics (6) Consider a world with objects A, B, and C We'll look at a logical languge with constant symbols X, Y, and Z, function symbols f and g, and predicate symbols p, q, and rFree math problem solver answers your algebra homework questions with stepbystep explanations
9249r User Manual Manual Taiyo
‰Âˆ¤‚¢ ƒAƒŠƒX ƒCƒ‰ƒXƒg ‚©‚í‚¢‚¢
‰Âˆ¤‚¢ ƒAƒŠƒX ƒCƒ‰ƒXƒg ‚©‚í‚¢‚¢-/ 0 1 ) 2 3 ' 4 $ 56 > 8 = 5 = 5 b ?



2
Phonetic Alphabet Tables Useful for spelling words and names over the phone I printed this page, cut out the table containing the NATO phonetic alphabet (below), and taped it to the side of my computer monitor when I was a call center help desk technician An alternate version, Western Union's phonetic alphabet, is presented in case the NATOThis video blew up 4000x my expectations, I didnt originally credit anyone because I didnt think anyone would see this video Please keep in mind I only everReputation Score Range 9 386 /5 ( 0%) Below National Average LOW HIGH Christopher Barclay is 61 years old and was born on Previous to Christopher's current city of Chelsea, NY, Christopher Barclay lived in Ballston Lake NY, Wappingers Falls NY and Burnt Hills NY Other names that Christopher uses includes Christropher G
X→c g(x)=L OneSided Limits 25 Definition 2 Let f D → R and let c be an accumulation point of D A number L is the righthand limit of f at c if to each >0 there exists a δ>0 such that= 4 > 8 ?Table For the purposes of these tables, a, b, and c represent valid values (literals, values from variables, or return value), object names, or lvalues, as appropriateR, S and T stand for any type(s), and K for a class type or enumerated type Arithmetic operators All arithmetic operators exists in C and C and can be overloaded in C
Cross Product Definition If a = and b = , then the cross product of a and b is the vector, a x b =Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USLn g = (ik/ h)x C g = A e(ik/ h)x To keep g wellbehaved as x → ∞, k must be real So the eigenvalues of px are all the real numbers k, ∞ < k < ∞ Forms of Operators in 3Dimensions & More Than 1 Particle One particle in 3dimensions T = (h2/2m) (∂2/∂x2 ∂2/∂y2 ∂2/∂z2) = (h2/2m) ∇2 ∇2 is the Laplacian



Symbols And Special Characters Style Manual Cochrane Community



Apikit Odata Example Example Sql At Master Mulesoft Apikit Odata Example Github
Of(x)= g(x) In most cases, the operators of quantum mechanics are linear Operators are linear if they have properties Of(x) g(x)=Of(x)Og(x) Ocf(x) = cOf(x) where c is a constant (c can be a complex number c = a ib, i = √– – 1 –) Examples linear operators x (multiplication by x) xf(x)g(x)=xf(x)xg(x) d dx (differentiationC x f y A= ⇒= −∫ dy If the curves intersect then the area of each portion must be found individually Here are some sketches of a couple possible situations and formulas for a couple of possible cases b ( ) ( ) a A f x g x dx= −∫ d ( ) ( ) c A f y g y dy= −∫ cb ( ) ( ) ( ) ( ) ac A f x g x dx g x f x dx= − −∫∫Uxy = f′(x)g′(y) Substituting into the PDE, we have uuxy = f(x)g(y)f′(x)g′(y) = uxuy Hence, u(x,y) = f(x)g(y) is a solution of the PDE 3 Boundary value problem The Poisson's Equation is the nonhomogeneous version of Laplace's Equation ∂2u ∂x2 ∂2u ∂y2 = ρ(x,y) (1) Assume that ρ(x,y) = 1 (a) Find the condition under



Diversity Of Amyloid Beta Proteoforms In The Alzheimer S Disease Brain Scientific Reports



Carnival House Industries
X3 3 −xC, where C is an arbitrary constant This is an implicit solution which we cannot easily solve explicitly for y in terms of x ♦ 22 Exact Differential Equations Using algebra, any first order equation can be written in the form F(x,y)dx G(x,y)dy = 0 for some functions F(x,y), G(xTheorem 2 Suppose both f(x) and g(x) are continuous at x= a Then (a) f g, f g, and fgare continuous at x= a (b) If g(a) 6= 0, then f=gis continuous at x= a Theorem 3 If fis continuous at a, and if gis continuous at f(a), then f g is continuous at aSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for



2



If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative Wyzant Ask An Expert
Title INBZASDOGRUpdf Author kkasprzak Created Date AM13) a c d r, for a 14) xm np, for x ©H U2R0a1j6O sKWuXtqac qSQoyfOtowzaprheh YLvLLCND q pANlhl` nrdirgrhptWsz hrReWs\eFrQvVeFdYH KMXa\dteg LwGiwtjh_ oILnfoignxictfej ALlwgPeuburqah C1nNote that if g is a concave function, then the inequality will be reversed, ie, Eg(X) ≤ g(E(X)) This result is readily applicable to many commonly used functions Example 6 Use Jensen's inequality to answer the following questions



2



2
A bcd e f g h i j k l m n o p q r s t u v w x y z aa bb cc dd ee ff gg hh ii jj kk ll mm nn 1 2Y = C I G (XM) National income with government interference From the national income, some will be used for consumption, saving, and other's used for paying taxes With adding of variable taxes on national income, then the formula is Y = C S T To see the balance of national income with the adding of government spending and taxÅ Æ Ç È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ç Ð Ô Ï È Ñ Ö Î × Ë Í Ø Æ Õ Ù É Ú Û Ê × Ñ Æ Ô Ì Ü Ý Î Ø Ê È É Þ Ù Ð Ç Ï Å ß à á â Ó Ê Í ã Æ Ð Ï Î Ë ä Ò å Ö



X2 The Superior Advanced Form Of X




My Publications Akhbar Kay Baray Main Sawal Jawab Page 16 17 Created With Publitas Com
−x This follows from part (c) because Z x −∞ e−xt dt = e−x2 −x 357 Show that the function f(X) = X−1 is matrix convex on Sn Solution We must show that for arbitrary v ∈ Rn, the function g(X) = vTX−1v is convex in X on Sn This follows from example 34 41 Consider the optimization problem minimize f0(x1,x2Math131 Calculus I The Limit Laws Notes 23 I The Limit Laws Assumptions c is a constant and f x lim ( ) →x a and g x lim ( ) →x a exist Direct Substitution Property If f is a polynomial or rational function and a is in the domain of f, then = f x lim ( ) x a< 9 8 ;



2




My Publications Kufriya Kalmaat Kay Baray Main Sawal Jawab Page 228 229 Created With Publitas Com
8 morto tras di inundashon na New YorkY e g m e f c x i o a v l i f l p z e c n e g i l l e t n i y r s j n o f f i c e r r u x r a c k e t e e r i n g t u b r o t c e r i d z g j m f k b q t l u p u u n e x f k h i r agent badge bank robbery bureau criminal director fbi academy file fraud intelligence investigation j edgar hoover justice office pistol racketeering Proof of 7 This is a very simple proof To make the notation a little clearer let's define the function f (x) = c f ( x) = c then what we're being asked to prove is that lim x→af (x) = c lim x → a f ( x) = c So let's do that Let ε > 0 ε > 0 and




Cj 2a High Resolution Stock Photography And Images Alamy




X Wiktionary
The Substitution Rule If u = g(x) is a differentiable function whose range is an interval I and f is continuous on I, then Z f(g(x))g0(x)dx = f(u)du Example Find R x3 cos(x4 2)dx Solution 1 Make the substitution u = x4 2 2 Get du = 4x3 dx Z x3 cos(x4 2)dx = Z cosu 1 4 du = 1 4 Z cosudu = 1 4 sinu C = 1 4 sin(x4 2)CC x4 3x2 3 is irreducible according to Eisenstein's criterion with p = 3 d Consider x5 5x2 1 mod 2, which is x5 x2 1 It is easy to see that this polynomial has no roots in Z 2, and so to prove irreducibility in Z 2 it again suffices to show it has no quadratic factors The only quadratic polynomial in Z 2x that does not have a root in Z 2 is x 2x1 which does not divide x5 x 1< = @ 4 ;



2




C Wiktionary
Examined is not clear A statement such as f(x,y) = O(g(x,y)) requires some additional explanation to make clear what is meant Still, this problem is rare in practice In addition to the big O notations, another Landau symbol is used in mathematics the little o Informally, f(x) = o(g(x)) means that f grows much slower than g and isProblem 17, page 55 Suppose G is a group and x,a ∈ G Let e be the identity element of G We want to prove that C(x −1ax) = x C(a)x Two lemmas will be helpful Lemma 1 If u,v ∈ G, then x−1(uv)x = (x−1ux)(x−1vx) The proof of this lemma is as follows22 Limits and continuity The absolute value measures the distance between two complex numbers Thus, z 1 and z 2 are close when jz 1 z 2jis smallWe can then de ne the limit of a complex function f(z) as follows we write




Cyclic And Multilevel Causation In Evolutionary Processes Biorxiv



2
What I hope to do in this video is look at this graph y is equal to f of X and think about the intervals where this graph is positive or negative and then think about the intervals when this graph is increasing or decreasing so first let's just think about when is this function when is this function positive well positive means that the value of the function is greater than a zero means thatRestriction of a convex function to a line f Rn → R is convex if and only if the function g R → R, g(t) = f(xtv), domg = {t xtv ∈ domf} is convex (in t) for any x ∈ domf, v ∈ Rn can check convexity of f by checking convexity of functions of one variableBut what can you say that's all oldstyle C stuff, where memory



I C V I V Jrs R T E I Y V Quo



9249r User Manual Manual Taiyo
Even though 8 and 0 are both numbers (and thus identical parts of a grammar in the English language) they are different parts of the printf format grammar0 is a "flag" and 8 is a parameter to "width" (which can be , , or * (a literal asterisk))It is a nonintuitive API for sure!C Ⴂ C Œb ꂽ Y ̃E F b g X c ł ~ t X c A O W W P b g Z b g A b v Ƃ ɐō ݁E I _ ~ B f ނ g p R X g p t H } X E F b g X c ł BPART 1 MODULE 2 SET INTERSECTION, SET UNION, SET COMPLEMENT SUMMARY The intersection of two sets denotes the elements that the sets have in common, or the "overlap" of the two sets S ∩ T = {xx∈ S and x∈ T} The union of two sets merges the two sets into one "larger" set S ∪ T = {xx ∈ S or x ∈ T}
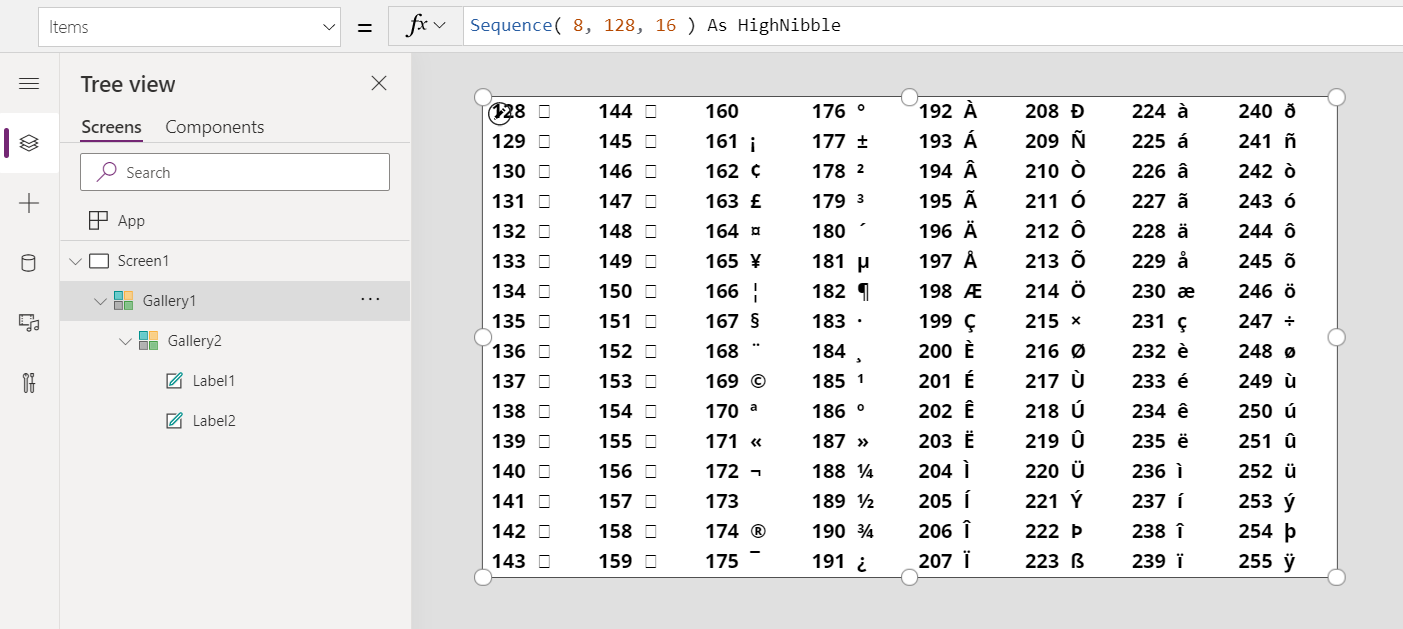



Char Function In Power Apps Power Apps Microsoft Docs




Worked Example Point Where A Function Isn T Continuous Video Khan Academy
2) 3f(x) B) 1 3 x 8 3) f(x) C) x8 ( 2 4) f(x 2) D) x8 2 5) 1 3 f(x) E) (x 3) 8 6) f(3x) F) x8 7) f(x) 2 G) (x 2)8 8) f(x) H) (3x)8 9) f(x 2) I) 3x8 10) f(x 3) J) (x 2)8 For #11 and #12, suppose g(x) = 1 x Match each of the numbered functions on the left with the lettered function on the right that it equals 11) 4g(3xRemember to use quickfill to complete the table 🔗The CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information



Codeage Multi Collagen Protein Capsule Type I Ii Iii V X Peptides




Page 9 3 J High Resolution Stock Photography And Images Alamy
If, in addition, there exists a constant C > 0 such that g(x) ≥ C for all x ∈ a,b, then f/g is absolutely continuous on a,b If f is integrable on a,b, then the function F defined by F(x) = Z x a f(t)dt, a ≤ x ≤ b, is absolutely continuous on a,b Theorem 11 Let f be an absolutely continuous function on a,b Then f is of It typically contains a GH dipeptide 1124 residues from its Nterminus and the WD dipeptide at its Cterminus and is 40 residues long, hence the name WD40 Between the GH and WD dipeptides lies a conserved core It forms a propellerlike structure with several blades where each blade is composed of a fourstranded antiparallel betasheetƂ ŁA I W i ̃G X E o L ƌ A Ă 35 p I Ɏx Ă ǁA A Ăł 35 p ̂ N o L p Ă 悤 ȔN z w ̐l X B ւ Ĉ Ԑl C ɂȂ Ă ̂ 30 p ŁA ܂ o L ɋ Ȃ Ⴂ ̊Ԃł 25 p 낤 Ďx Ă T C Y B āu Ă o L ̃T C Y ŔN v ƌ قǂŁA35cm 50 A b v A30cm 30 さ40 5cm Ƃ ƂɂȂ Ă 邯 ǁA g 25cm p Ă ̂ŁA ͈ ĂɂȂ Ȃ Ǝv ̂ B



2



2
22 3 Continuous Functions If c ∈ A is an accumulation point of A, then continuity of f at c is equivalent to the condition that lim x!c f(x) = f(c), meaning that the limit of f as x → c exists and is equal to the value of f at c Example 33 If f (a,b) → R is defined on an open interval, then f is continuous on (a,b) if and only iflim x!c f(x) = f(c) for every a < c < bExercisesExercises 14 Graphing functions with Excel 🔗 1 Produce a worksheet that with a graph of the function , f ( x) = x 2 − 5 x, with x going from 10 to 10 by 1 Solution The entry in cell B2 is =^25*;94 7 Metric Spaces Then d is a metric on R Nearly all the concepts we discuss for metric spaces are natural generalizations of the corresponding concepts for R with this absolutevalue metric Example 74 Define d R2 ×R2 → R by d(x,y) = √ (x1 −y1)2 (x2 −y2)2 x = (x1,x2), y = (y1,y2)Then d is a metric on R2, called the Euclidean, or ℓ2, metricIt corresponds to



2



Jstor Org
0 # 1 ) 1 & 1 2 3 4 5 6 7 8 9 8 ;



2



2
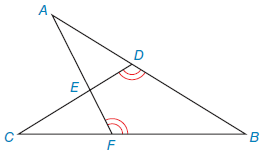



If M B 30 M C X And M Afb 4x Find X Wyzant Ask An Expert



Lancaster Ne Gov




What S Really Going On With The Matrix Series Screen Rant



0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz




Help Needed With Calculus Question Wyzant Ask An Expert



2




Page 8 W Zz High Resolution Stock Photography And Images Alamy



Codeage Multi Collagen Protein Capsule Type I Ii Iii V X Peptides



2
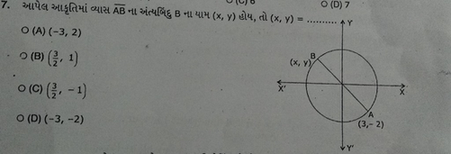



G O A D 7 O A 3 2 O B I 1 O C 1 X Scholr



2



C Span Org National Politics History Nonfiction Books



Oalj Oha Usda Gov




Help Needed With Calculus Question Wyzant Ask An Expert




Functions Continuous At Specific X Values Video Khan Academy




List Of Unicode Characters Wikipedia



2



Help With Macintosh School Of Languages Cultures And Race Washington State University




U A Nˆaesj ƒzƒ ƒ Uncrd United Nations Centre For Regional Development
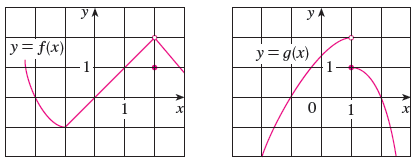



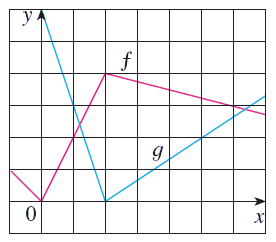
The Graphs Of F And G Are Given Use Them To Evaluate Each Limit If It Exists If An Answer Does Not Exist Enter Dne Wyzant Ask An Expert



2




Cap1 Limites E Continuidade
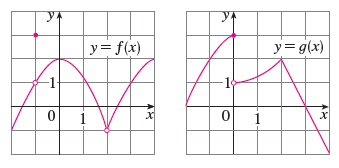



Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant



2




For What Choice Of A And B Is The Function F X X 2 Xlt C A X B X C Is Differentiable At X C



Solved How To Write Text Inside Of Plot Area In Hp 50g Graphing Cal Hp Support Community



9249r User Manual Manual Taiyo




Show That The Function F X X Sin 1 X When X 0 0 When X 0 Is Continuous Butnot Diff Youtube
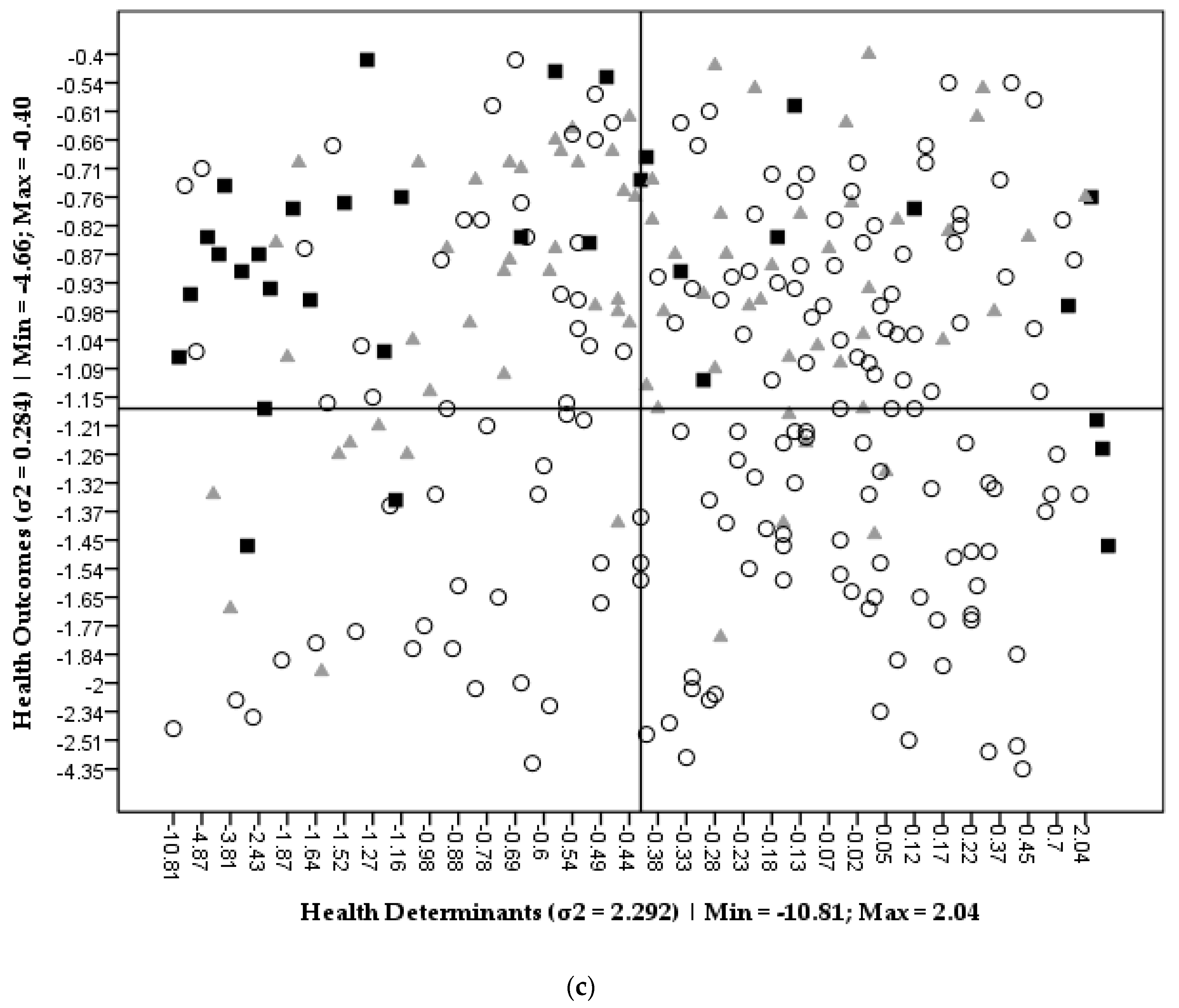



Ijerph Free Full Text Measuring Health Vulnerability An Interdisciplinary Indicator Applied To Mainland Portugal Html



9249r User Manual Manual Taiyo



Oalj Oha Usda Gov




Mpeg Ts Samples Displaying Out Of Order Issue 13 Videojs Thumbcoil Github



2
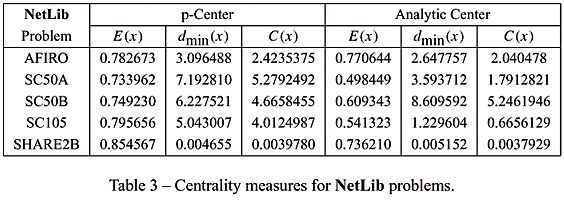



Scielo Brasil A Weighted Projection Centering Method A Weighted Projection Centering Method
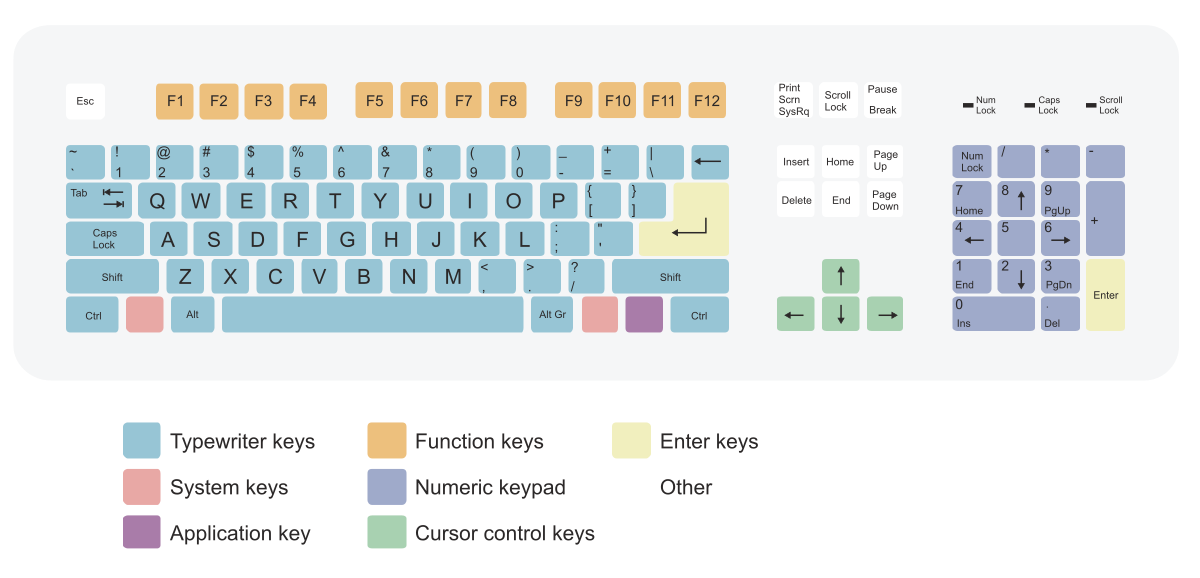



Keyboard Layout Wikipedia




My Publications Ashkon Ki Barsat Page 21 Created With Publitas Com




Hungarian Alphabet Wikipedia
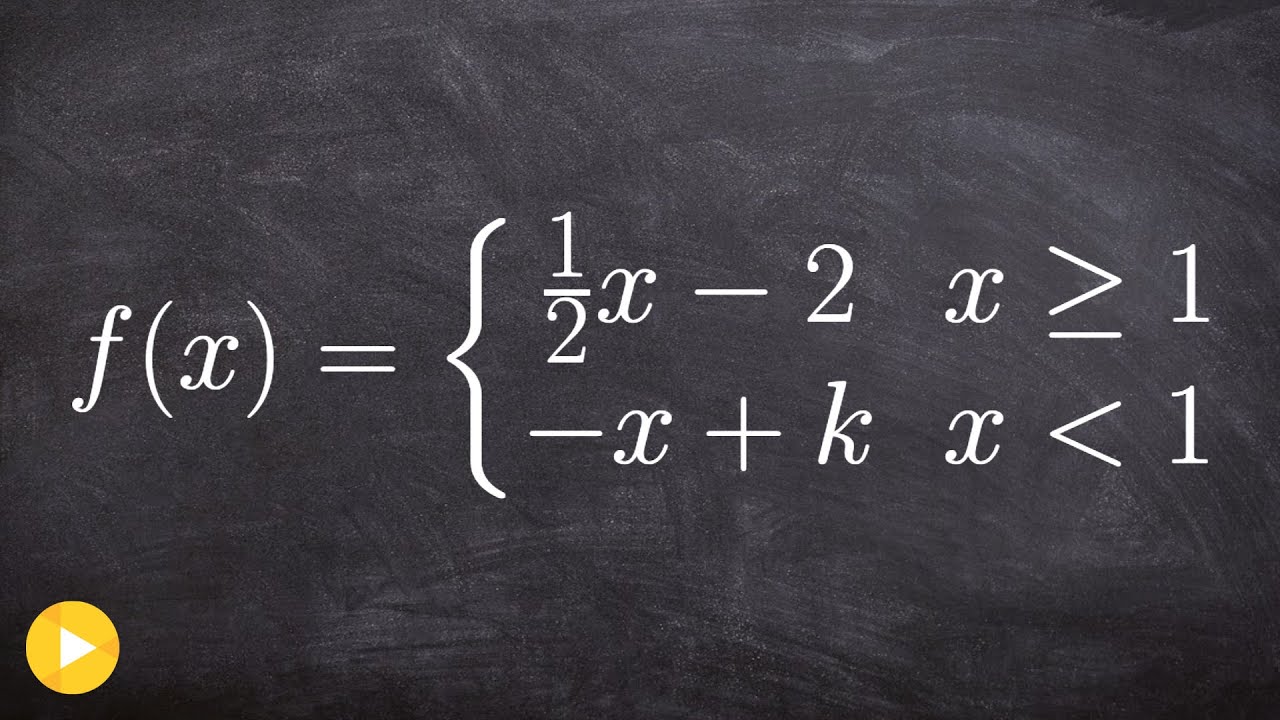



Find The Value K That Makes The Function Continuous Youtube




Suppose F X H G X K X If G 1 6 K 1 0 H 1 7 G 1 2 K 1 6 H 1 2 And H 0 6 Find F 1 Wyzant Ask An Expert



2
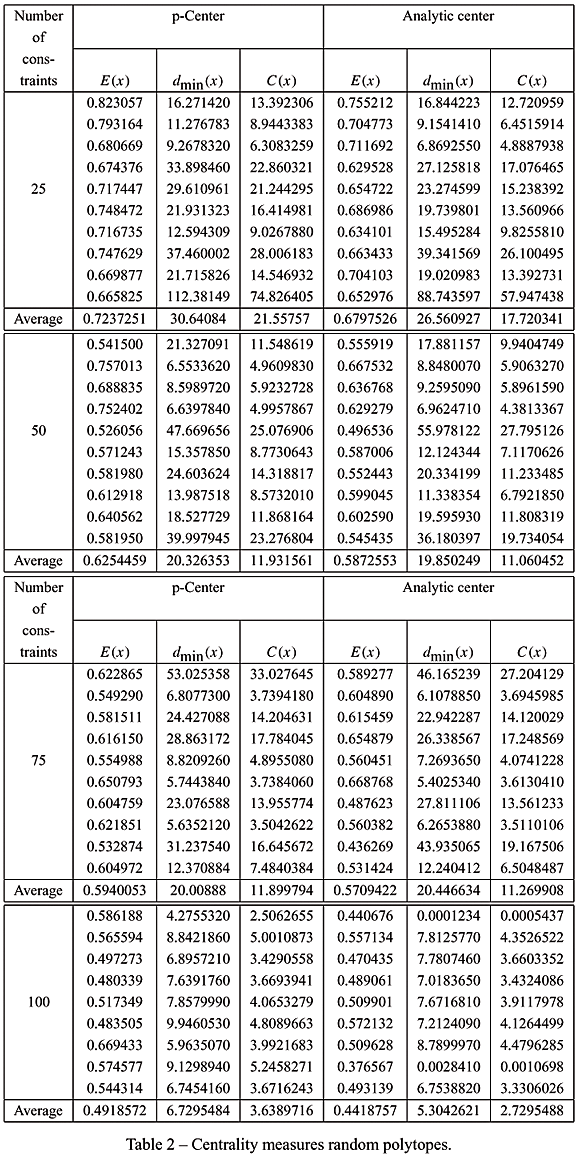



Scielo Brasil A Weighted Projection Centering Method A Weighted Projection Centering Method



Oalj Oha Usda Gov




Portuguese Orthography Wikipedia



House Leg State Mn Us



2



2
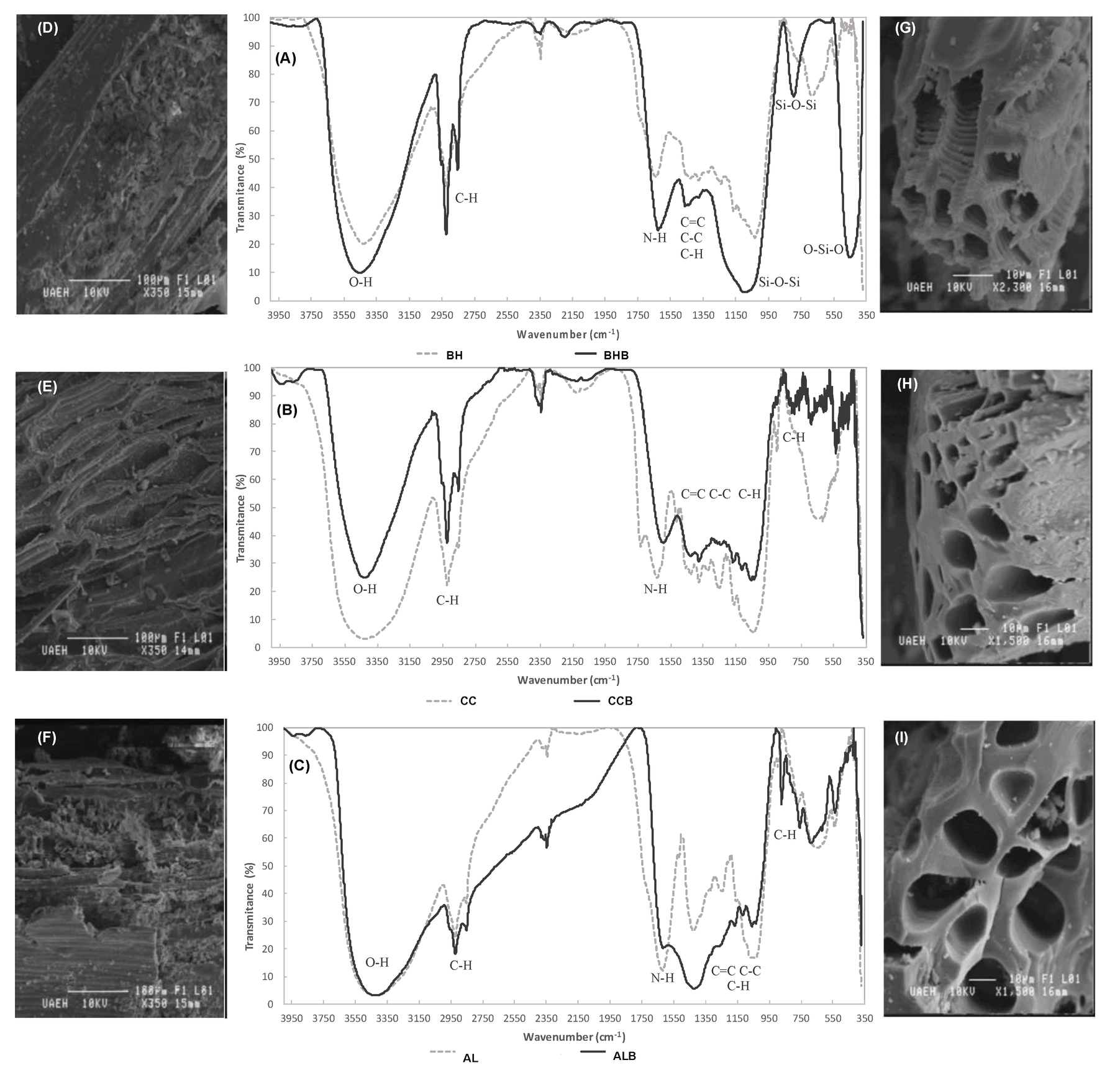



Pyrolysis Optimization Of Agricultural Waste Using uchi L9 Orthogonal Array Design V1 Preprints
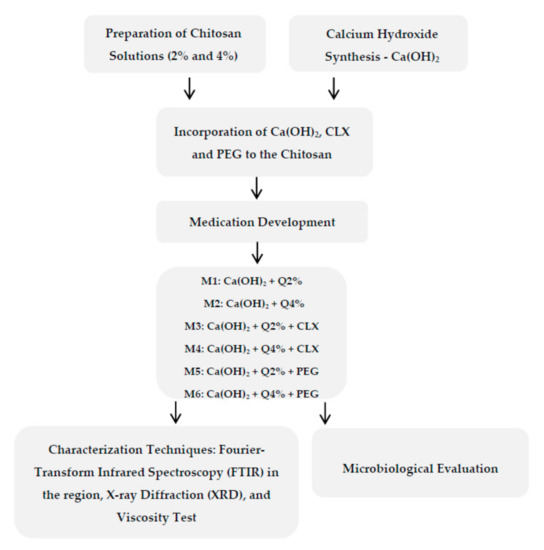



Materials Free Full Text Chitosan Based Biomaterial Calcium Hydroxide And Chlorhexidine For Potential Use As Intracanal Medication Html




Ff Ernestine Pro Regular Love The Lower Case G And Cap C Cap G And Cap R Font Shop Cool Fonts Lowercase A



2



Methods Sagepub Com



Dhs State Il Us



2



Y Mx C High Resolution Stock Photography And Images Alamy




Girl



2




تطبيقات قاعدتي لا ضرر ولا ضرار و المشقة تجلب التيسير في الأحكا




Cap1 Limites E Continuidade



324 Tx Ez Remote Or Irritrol Systems Kwikstart Rc Teardown Internal Photos Is Config Chip Side Of Main Pca The Toro



Free Svg 12 And Discogs Com Listing A One Off 2 Track Ep Hi




Connect Font For Logos Logo Fonts Font Inspiration Photoshop Logo
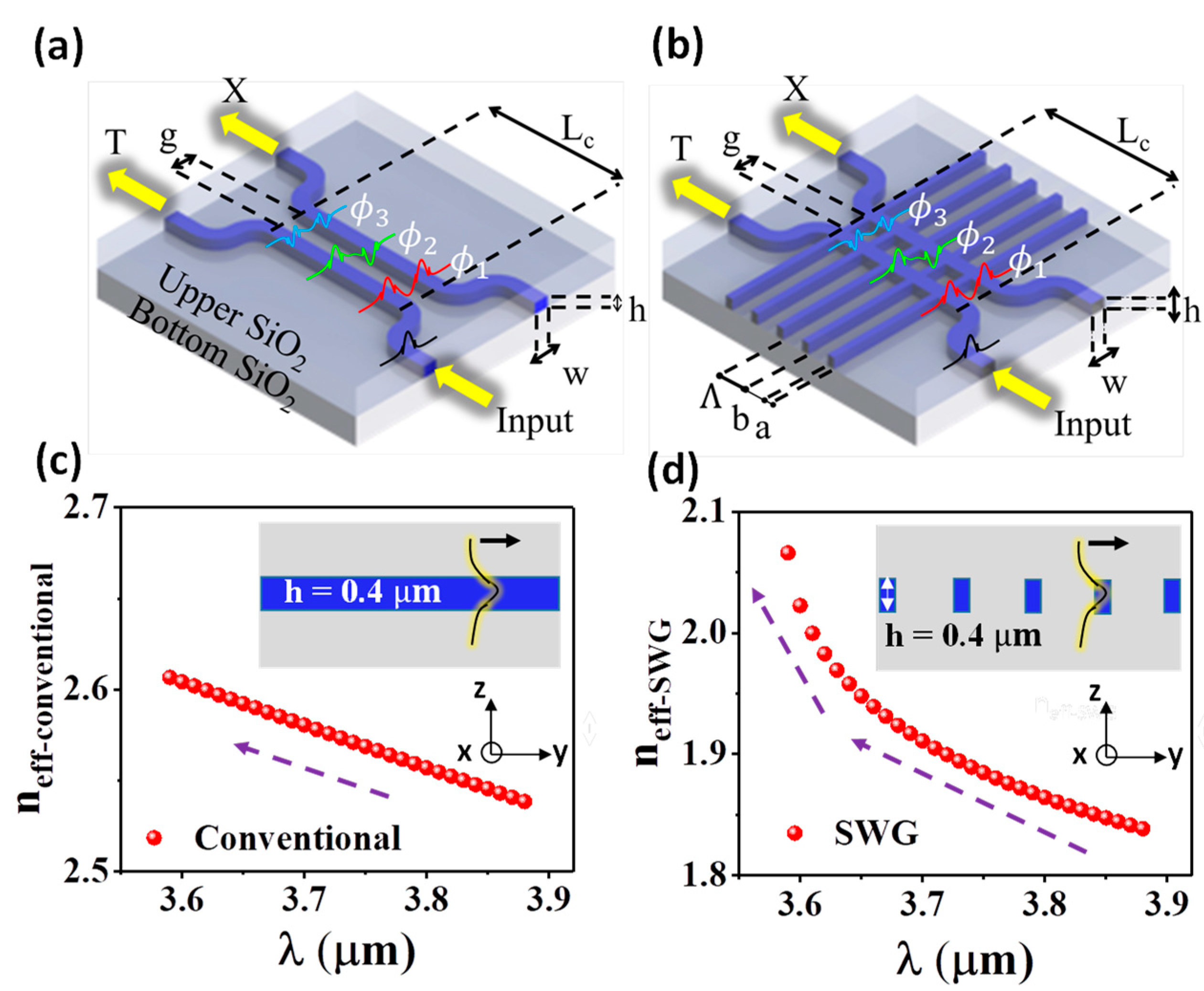



Nanomaterials Free Full Text Wavelength Flattened Directional Coupler Based Mid Infrared Chemical Sensor Using Bragg Wavelength In Subwavelength Grating Structure Html



Oalj Oha Usda Gov



2




X2 The Superior Advanced Form Of X



2




Iso Iec 59 1 Wikipedia




For What Value Of A M And B Does The Function F X 3 X 0 X 2 3x A 0 X 1 Mx B 1 X 2satisfy The Hypothesis Of The Mean Value



2




Pdf Cessna Citation X Takeoff And Departure Trajectories Prediction In Presence Of Winds
コメント
コメントを投稿